First appearing in 1869, the “n-queen problem” has puzzled scientists for over 150 years.
Chess is an ancient game originating from India and Persia, which began to emerge in Southern Europe in the latter half of the 15th century. Despite its long history, chess still holds many mysteries, the most famous of which is the n-queen problem, derived from a puzzle.
Chess is an ancient game originating from India and Persia.
The puzzle is as follows: How many ways can 8 queens— the most powerful pieces on the board that can move any number of squares horizontally, vertically, or diagonally—be positioned on a standard 64-square chessboard without any queen being in a position to “block” another.
This puzzle first appeared in 1848, posed by chess master Max Bezzel in the German chess magazine Schachzeitung. From the moment it was mentioned, the puzzle has caused many chess enthusiasts, and even mathematicians, to struggle with finding a solution.
The answer was revealed two years later, with the solution being that there are 92 ways to arrange 8 queens on the board, but to summarize, there are only about 12 basic arrangements, as most of the other solutions are symmetrical to each other.
However, in 1869, a variant of this puzzle was posed by mathematician Franz Nauck, and it was even more complex. The problem asks: Instead of arranging 8 queens on a standard 8 x 8 board, what if there were 1,000 queens on a 1,000 x 1,000 board? Then 1 million, 1 billion…
What was once a relatively simple puzzle has become a much deeper problem, as it requires discovering the general rule for the number of arrangements of any number (denoted as “n”) of queens on an n x n board.
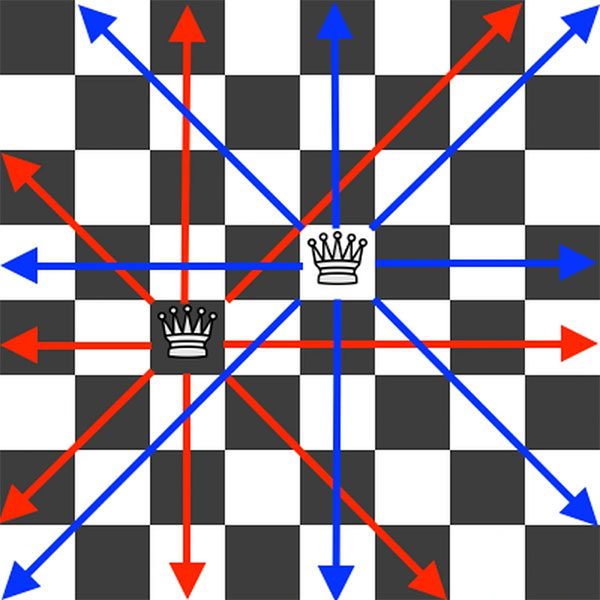
The problem involves arranging queens on a chessboard so that piece A is not on the attack path of piece B.
Until now, after more than 150 years, Michael Simkin, a mathematician at the Harvard University Center for Mathematical Sciences and Applications, has provided what is considered a nearly accurate answer to this problem.
Specifically, according to Simkin, on a giant chessboard with an n x n coefficient, there are approximately (0.143n) ^ n ways to arrange n queens so that no queen can attack another. This means that on a million x million board, the arrangements for 1 million queens could reach a number consisting of 5 million zeros.
It is known that Simkin spent nearly 5 years to find this approximate equation. His method for solving the problem involves placing a queen randomly on the board, then blocking all squares it can reach (including squares vertically, horizontally, and diagonally). After that, he continues to use an algorithm to arrange the remaining queens in a similar manner.
However, this algorithm is not perfect, as it works best on symmetrical problems where every square provides the same attacking advantage for the queen as any other square. This is not the case on a standard chessboard, where queens positioned on squares near the edge have significantly less attacking power than those in the center.
To address this issue, Simkin realized that he would need to make further adjustments to the algorithm, but he has come closer to conquering this challenge.
“I think that personally I might solve the n-queen problem in some time,” Simkin said. “Not because there’s nothing left to do, but simply because I have always dreamed of chess variants and I am ready to continue my passion.”
