Mathematics is the study of concepts such as quantity, structure, change, and space. Some groundbreaking mathematical concepts have not only changed the course of human history but have also profoundly transformed the world we live in!
Mathematical equations are often seen as a window for humanity to peer into the universe; they have practical significance and help us see things we have not noticed before. Therefore, new advancements in mathematics often accompany improvements in our understanding of the cosmos. Next, let’s explore 9 famous equations in history that have completely altered how humans perceive the world.
Pythagorean Theorem
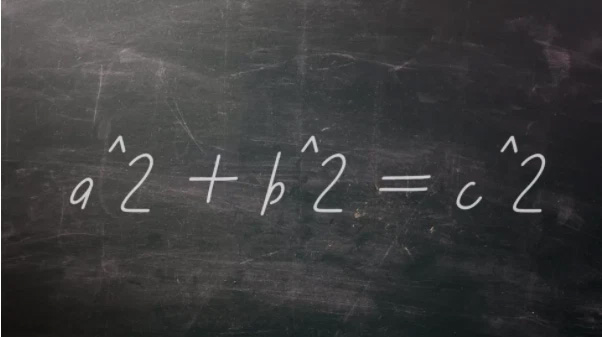
The first important trigonometric function that everyone learns in school is the relationship between the lengths of the sides of a right triangle. The sum of the squares of the two legs equals the square of the length of the hypotenuse. This theorem is often written as: a² + b² = c² and has existed for at least 3,700 years, dating back to Babylon.
The Pythagorean theorem is one of the significant mathematical theorems discovered and proven in early human history. Researchers at the University of St Andrews in Scotland believe that the ancient Greek mathematician Pythagoras wrote down the form of the equation widely used today, and the modern Western mathematical community refers to it as the “Pythagorean Theorem.”
In addition to its applications in architecture, navigation, mapping, and other critical processes, the Pythagorean theorem has helped expand the concept of numbers. In the 5th century BC, the mathematician Hippasus from Metapontum discovered that if the two legs of an isosceles right triangle are each 1, then the length of its base is the square root of 2, which is an irrational number. According to a paper from the University of Cambridge, Hippasus was allegedly thrown into the sea because people at the time were too shocked and frightened by the so-called “irrational number.” At that time, Pythagoreans believed that only whole numbers and fractions (rational numbers) existed in the world.
F = ma and the Law of Gravitation
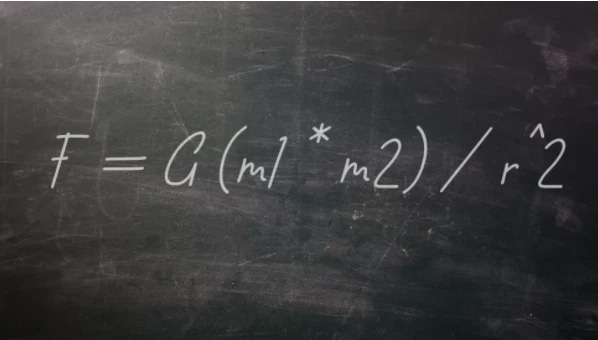
Isaac Newton is one of the most prominent figures in the history of British and even human science. He made many discoveries that changed the world, including his second law of motion. This law is typically written as F = ma. An extension of this law, combined with other experimental observations, allowed Newton in 1687 to describe what we now call the law of universal gravitation: F = G (m1 * m2) / r². Records show that Cavendish was the first to complete an experiment measuring the gravitational force between two objects in the laboratory, accurately obtaining the gravitational constant and the mass of the Earth. Others later used the experimental results to derive the density of the Earth.
Newton’s second law is dubbed the soul of classical mechanics; it can govern the motion of various objects and physical phenomena, and its applications are widespread. Many concepts from Newton’s laws of motion are also used to understand many complex physical systems, including the motion of planets in the solar system and how rockets are used for movement.
Wave Equation
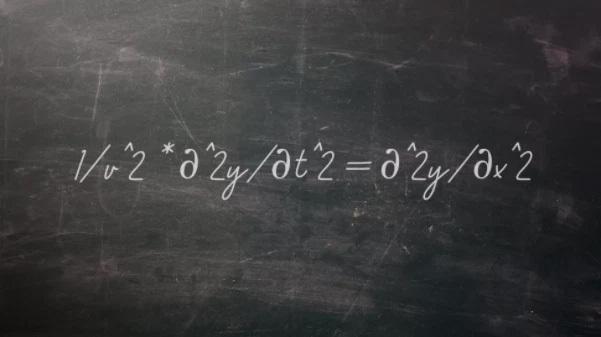
Using Newton’s laws of motion, 18th-century scientists began analyzing everything around them. The French physicist, mathematician, and astronomer Jean le Rond d’Alembert deduced in 1743 and developed an equation describing the phenomenon of vibrations of strings or waves. This equation can be written as:
1 / v² * ∂²y / ∂t² = ∂²y / ∂x²
In this equation, v is the wave velocity, and the other parts describe the displacement of the wave in one direction. Using the wave equation extended to two or more dimensions, researchers can predict the movement of water, seismic waves, and sound waves. This equation also forms the basis for the Schrödinger equation in quantum physics, which makes many modern computing devices feasible.
Fourier Equation

Whether you have heard of the French mathematician and physicist – Baron Jean-Baptiste Joseph Fourier or not, his work has undoubtedly shaped your life. The mathematical equations he wrote in 1822 allowed researchers to break down complex, messy data into combinations of simple waves for easier analysis.
According to an article in the Yale Scientific Journal, the fundamental idea of the Fourier transform was a radical concept when proposed, and many scientists refused to believe that complex systems could be simplified. However, the Fourier transform has numerous applications in many fields of modern science, including data processing, image analysis, optics, communications, astronomy, engineering, finance, cryptography, oceanography, and quantum mechanics. For example, in signal processing, a typical use of the Fourier transform is to separate a signal into its amplitude and frequency components.
Maxwell’s Equations
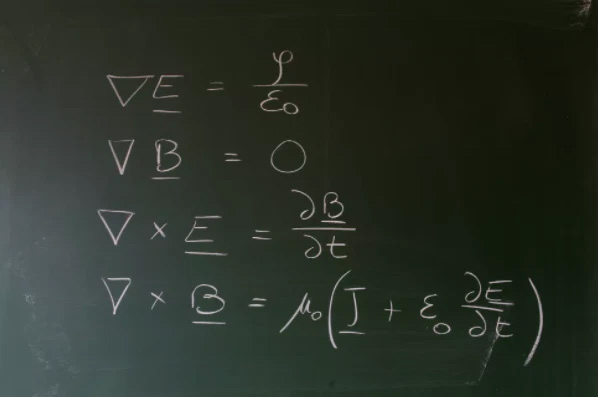
Electricity and magnetism were new concepts in the 19th century when scholars were studying how to harness and exploit these strange physical phenomena. In 1864, Scottish mathematician and physicist James Clerk Maxwell published a system of 20 equations describing how electric fields and magnetic fields work and how they relate to each other. This system of equations greatly contributed to our understanding of both phenomena.
Currently, Maxwell’s equations consist of four first-order linear partial differential equations, namely Gauss’s law, which describes how electric charges create electric fields; Gauss’s law for magnetism, which shows that there are no magnetic monopoles; and Faraday’s law of induction, which explains how a time-varying magnetic field generates an electric field.
E = mc²
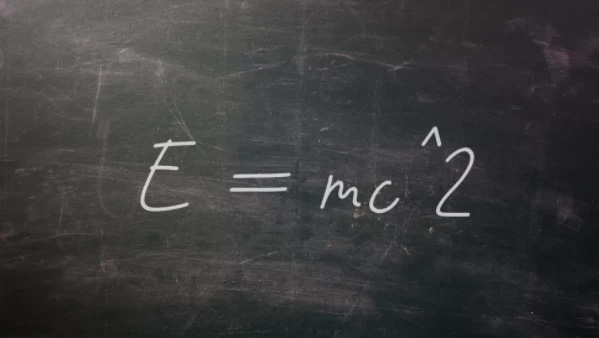
In 1905, Albert Einstein first proposed the mass-energy equivalence concept, E = mc², as part of his groundbreaking theory of special relativity. E = mc² shows that matter and energy are two sides of the same coin; in the equation, E represents energy, m represents mass, and c represents the constant speed of light.
Without E = mc², we would not be able to understand the existence of stars in the universe, nor would we know how to construct the Large Hadron Collider, a massive particle accelerator, and we would even be unable to glimpse the nature of the subatomic world. It can be argued that this equation has become one of the most famous equations in human history and has become a part of human culture.
Friedmann Equation
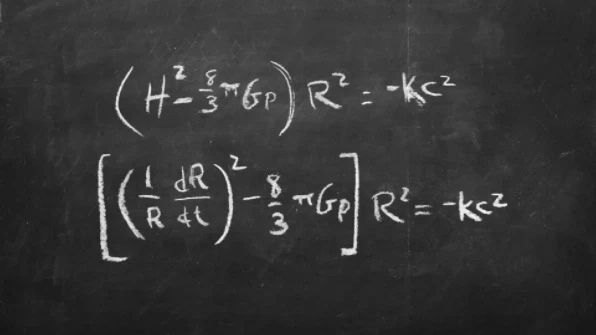
Defining the entire universe in the form of a set of equations might sound like an absurd idea, but that was the grand idea of Russian physicist Alexander Friedmann in the 1920s. Using Einstein’s theory of relativity, Friedmann indicated that since the Big Bang, the properties of the expanding universe could be represented by two separate equations.
These two equations incorporate all the important parameters of the universe, including the curvature of the universe, how much matter and energy the universe contains, and the rate at which the universe is expanding, along with crucial constants such as the speed of light, gravitational constant, cosmological constant, and Hubble constant. This is a model describing a homogeneous and isotropic expanding universe within the framework of general relativity.
Researchers believe that the cosmological constant, although small, may not be zero; and this constant may exist in the form of dark energy, which drives the accelerated expansion of the universe.
Shannon’s Information Equation
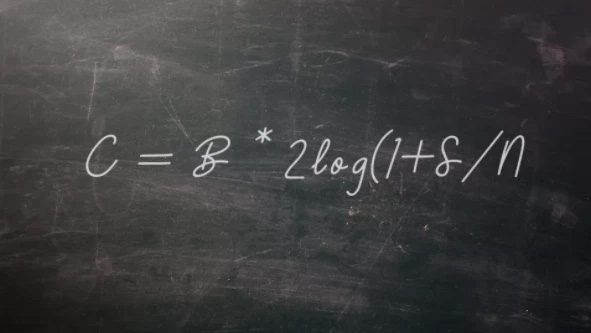
Most people are familiar with the 0s and 1s that make up binary numbers on computers. But this key concept would not have developed without the pioneering work of American mathematician and engineer Claude Shannon.
In a 1948 paper, Shannon proposed an equation for the maximum efficiency of information transmission, commonly written as: C = B * 2log (1 + S / N). Here, C represents the highest error-free data rate that can be achieved by a specific communication channel, B is the channel bandwidth, S is the average signal power, and N is the average noise power (S / N represents the signal-to-noise ratio of the system). The output of this equation is measured in bits per second (bps). In his 1948 paper, Shannon referred to a bit as an abbreviation for “binary digit” and attributed this concept to mathematician John W. Tukey.
Robert May’s Equation and Chaos Theory
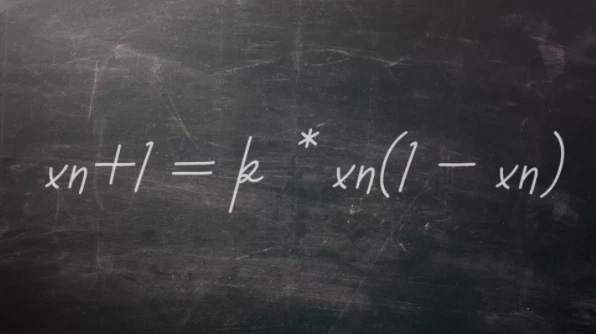
Simple concepts can sometimes lead to unexpectedly complex results. However, it wasn’t until the mid-20th century that scientists fully grasped the significance of this idea. At that time, the field of chaos theory was emerging, and researchers discovered that systems always possess a component that can generate random and unpredictable behavior. In 1976, Australian physicist, mathematician, and ecologist Robert May published a paper titled “Simple Mathematical Models with Very Complicated Dynamics” in the journal Nature. This paper proposed the equation: xn + 1 = k * xn (1 – xn), which describes the time-dependent changes of a quantity. This is a classic example of chaotic phenomena arising from simple nonlinear equations.
Subsequently, Robert May’s equation was used to explain population dynamics in ecosystems and to program computers to generate random numbers.