Scientists from the University of New South Wales have discovered the purpose of the famous 3,700-year-old Babylonian clay tablet, revealing it to be the oldest and most accurate trigonometric table in the world.
The Pythagorean Theorem is one of the most basic and well-known mathematical formulas taught to students everywhere. It states that in a right triangle, the square of the length of the hypotenuse (the longest side of the triangle) is equal to the sum of the squares of the lengths of the other two sides. The formula is often expressed as a² + b² = c², where a, b, and c represent the lengths of the sides.
This theorem is named after Pythagoras, a Greek philosopher and mathematician who lived in the 6th century BC. However, recent discoveries indicate that Pythagoras was not the first to understand the relationship between the sides of a right triangle. In fact, the ancient Babylonians discovered the Pythagorean theorem over 1,000 years before Pythagoras was born!
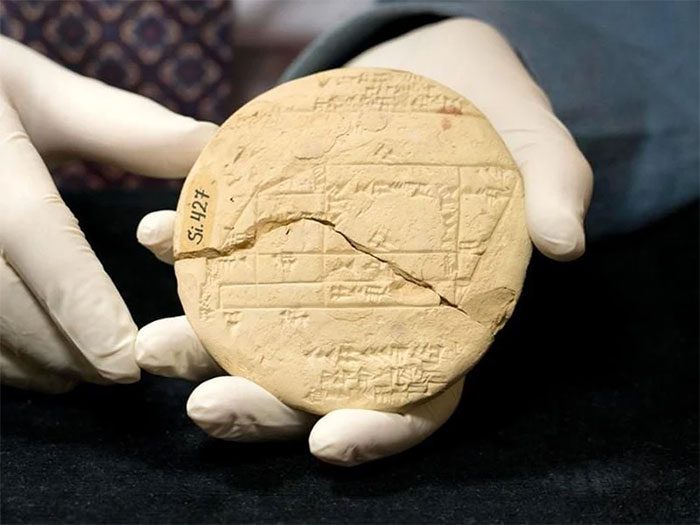
The tablet Si.427, the oldest known example of applied geometry.
How do we know this? Evidence comes from clay tablets found in what is now Iraq, dating back to ancient Babylon (1900-1600 BC). These clay tablets contain calculations and mathematical diagrams that utilize the principles of the Pythagorean theorem to solve problems related to land surveying, construction, and astronomy.
One of these clay tablets, known as Si.427, is considered the oldest known example of applied geometry. Excavated in 1894 in present-day Iraq, it features a diagram of four adjacent right triangles within a square, alongside descriptions of land boundaries and features inscribed in cuneiform script. The tablet employs a set of numbers now referred to as Pythagorean triples, which are sets of positive integers that satisfy the Pythagorean equation. For instance, 3, 4, and 5 form a Pythagorean triple, as 3² + 4² = 5².
Another tablet, known as Plimpton 322, contains a table of 15 rows and four columns of numbers representing Pythagorean triples. This tablet was discovered by American archaeologist Edgar Banks in 1922 and is currently housed at Columbia University in New York. Mansfield, a mathematician at the University of New South Wales, along with colleague Norman Wildberger, published a paper in 2017 arguing that Plimpton 322 may have been used in the construction of canals, palaces, and temples, or perhaps in land surveying.

Plimpton 322, a 3,700-year-old Babylonian clay tablet housed in the Rare Manuscripts and Special Collections Library at Columbia University in New York.
The solution to this puzzle was revealed through Si.427. Mansfield happened upon this clay artifact at the Istanbul Archaeological Museum, where it had been quietly stored for many years and was largely overlooked.
Mansfield stated: “With this new clay tablet, we can finally see why the ancient Babylonians were interested in geometry: to accurately define land boundaries.” “This was a time when land began to become private – people started thinking of land in terms of ‘my land and your land,’ wanting to establish proper boundaries for positive neighborly relations.”
Additional supporting evidence has also been found in the clay tablet IM67118, which dates back to 1770 BC. This discovery includes text, diagrams, and tools for calculating the area of rectangles as well as their diagonal lengths. The accompanying text outlines a solution using the Pythagorean theorem.

The clay tablet IM67118 presents a geometric-algebraic approach to solving problems, with conclusions reminiscent of the Pythagorean theorem.
Interestingly, the Pythagorean theorem also appeared in ancient India, emerging in the 8th century BC in the Sanskrit text known as the Sulbasutras, written by Baudhāyana. According to some scholars, this theorem, also identified in China as GouGu, may predate commonly understood knowledge, potentially being transmitted orally from around 2000 BC.

The ancient Babylonians made significant contributions to mathematics, particularly in the field of geometry. They utilized a sexagesimal system based on the number 60 and developed trigonometry. They also made advancements in astronomy and astrology, employing mathematical models to track the planet Jupiter and developing timekeeping methods still in use today.
The Greeks are often credited with inventing trigonometry (the branch of mathematics related to angles and distances in triangles), but Mansfield and Wildberger argue that the ancient Babylonians had their own version of trigonometry based on ratios rather than angles. They used a base-60 numbering system (similar to how we use minutes and seconds to measure time) to express these ratios with high accuracy.
Mansfield remarked: “The Greeks developed their trigonometry because they were studying astronomy, but the Babylonians had their own variant of trigonometry that they developed to solve land and boundary issues.”
These discoveries reveal that the ancient Babylonians were not only skilled mathematicians but also practical problem solvers who applied their knowledge to real-world situations. They challenge the common assumption that Pythagoras was the first to discover the Pythagorean theorem and demonstrate that mathematical ideas can emerge independently across different cultures and eras.