The Banach-Tarski Paradox is an important result in the field of set theory and geometry, first articulated by two Polish mathematicians, Stefan Banach and Alfred Tarski, in 1924.
In 1924, Polish mathematicians Stefan Banach (1892-1945) and Alfred Tarski (1901-1983) discovered a surprising mathematical truth: “You can divide a ball into a finite number of pieces and reassemble those pieces to create two balls that are the same size as the original ball.” In other words, if you split and smash a ball and then put it back together, you can end up with two identical balls! Here, although deformations such as stretching and shrinking are prohibited for the divided pieces, they can be moved and rotated when reassembling.

The Banach-Tarski Paradox was first published by Banach and Tarski in 1924. Their work built upon earlier discoveries by the Austrian mathematician Felix Hausdorff, who demonstrated a similar paradoxical decomposition for certain subsets of Euclidean space. Banach and Tarski expanded upon Hausdorff’s work to prove their astonishing result for three-dimensional spheres. The Banach-Tarski Paradox is a theorem in geometric set theory, stated as follows: “Given a solid ball in three-dimensional space, there exists a decomposition of the ball into a finite number of disjoint subsets which can then be reassembled in a different way to create two identical copies of the original ball.”
Most people would think: “How can this possibly happen?” In fact, because this discovery was so difficult to comprehend, it was initially labeled a paradox. However, today its validity has been mathematically proven, and it is referred to as the “Banach-Tarski Theorem.”
However, this theorem does not mean that if you take a tennis ball at home and break it into pieces, you can cleverly reassemble it into two tennis balls. The “decomposition” mentioned in this theorem is a special method that does not apply in the real world. Professor Shinya Koyama from Toyo University in Japan, who conducts research in number theory and other fields, stated: “Although this theorem uses the term ‘divided parts,’ in reality, it is considered infinite like thin clouds or fog; a dot would be more appropriate.”

The Banach-Tarski Paradox is a consequence of the Axiom of Choice, an important and controversial principle in set theory. While the Axiom of Choice has many useful applications in mathematics, it also leads to some bewildering results, such as the Banach-Tarski Paradox.
So why did these two scientists conceive such a paradox? The context was that there was a debate within the mathematical community at the time about the validity of the “Axiom of Choice.” This is a very complex mathematical topic, so let’s briefly outline it here.
The Axiom of Choice is one of the axioms in “set theory” and was published by the German mathematician Ernst Zermelo (1871-1953) in 1904. Set theory refers to the field that uses numbers, formulas, symbols, etc., to examine the properties of “sets” that contain different elements.
The content of the Axiom of Choice states: “If a set consists of many subsets (a set consisting of only a portion of the elements of that set), then it is possible to choose one element from each subset to form a new set.” Many would consider this self-evident. Georg Cantor, the German mathematician who laid the foundation for set theory, also believed that the Axiom of Choice was a given. In fact, when the number of subsets is finite, selecting elements from each subset is not problematic.
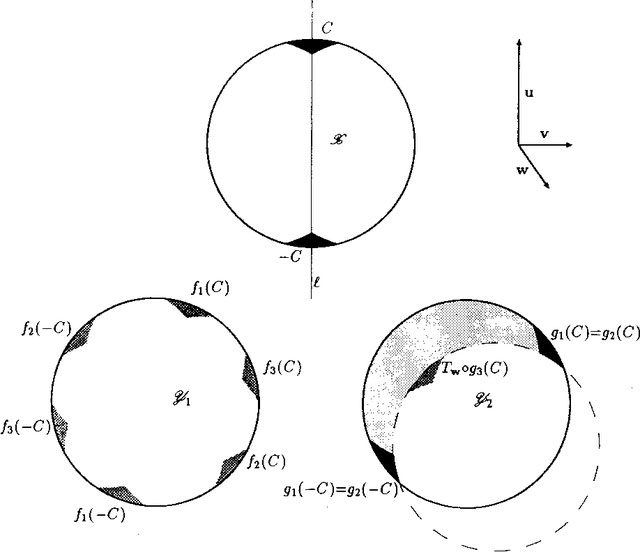
Another form of the theorem states that with any two “reasonable” solid objects (such as a small ball and a large ball), the pieces cut from one object can be reassembled into the other object. This is often informally stated as: “a pea can be cut into pieces and reassembled into the Sun,” and is referred to as the “pea and Sun paradox.”
However, if the number of subsets is infinite, then the operation of selecting elements also requires an infinite number of steps. Thus, the operation of selecting elements cannot be completed, and it is unclear whether a new set can be formed. As a result, the debate over the validity of the Axiom of Choice continued for many years.
In this context, using the Axiom of Choice leads to the conclusion that gives rise to the Banach-Tarski Paradox. When decomposing the ball (selecting a portion of the points that make up the ball to form a new set), you need to employ the Axiom of Choice.
Eventually, the debate over the Axiom of Choice heated up and finally concluded in 1938. The Czech-born mathematician Kurt Gödel (1906-1978), famous for his “Incompleteness Theorem,” proved that “even if the Axiom of Choice is true, it will not lead to new contradictions in set theory.” Based on this, “The Banach-Tarski Paradox” ultimately became officially known as the “Banach-Tarski Theorem.”