The quality of roads is being upgraded daily, but few people pay attention to adjusting curves to minimize the effects of centrifugal force. This is the root cause of many “mysterious” accidents.
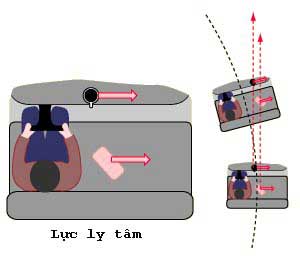 |
|
Centrifugal force causes objects in the vehicle to move opposite to the direction of travel. (Image: Hyperphysics) |
It is possible to identify curves where accidents frequently occur due to centrifugal force. Firstly, the curve from Thai Binh City to Diem Dien Town has a history of up to 20 accidents occurring simultaneously, where motorcycles and cars are pushed to one side of the road, crashing into trees or rolling into fields, causing vehicle damage and fatalities for both drivers and passengers.
The curved section of the railway on the Lang Co Pass is also in a similar situation; the curvature radius remains unchanged while the recommended travel time decreases, leading to increased train speeds. Without specific warnings or speed limits, accidents become inevitable.
Perhaps the most notable is the Phap Van – Cau Gie route, which has seen a number of unusual accidents recently. Some opinions suggest that the cause may be electromagnetic interference. However, according to Dr. Ha Duyen Chau, Deputy Director of the Institute of Geophysics, it is difficult to confirm this, as only a strong geomagnetic storm would impact human health. Dr. Chau stated: “On the Phap Van – Cau Gie route, if there are issues with the magnetic field, they are merely anomalies and not related to safe driving.”
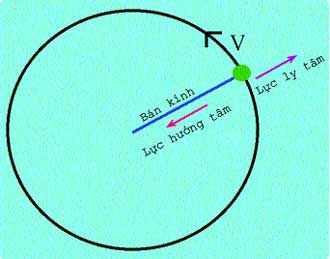 |
|
Components of centrifugal force. (Image: Apollo) |
The unusual accidents on the Phap Van – Cau Gie route are primarily caused by centrifugal force. The main reason is the unstable roadbed, which has many subsidence areas causing the surface to bulge and dip, resulting in an uneven road. Even more dangerously, these bulging and dipping sections follow one after the other. From the roadside, it is easy to spot such road segments. Vehicles traveling at high speeds on these kinds of roads will generate a standing centrifugal force acting on the vehicles. When a vehicle transitions from a bulging section to a dipping section, the vehicle’s weight, which was previously light, suddenly becomes very heavy, similar to compressing a ball, making the vehicle unstable, swaying, and rolling sideways. This process, if repeated several times, makes accidents understandable.
Below is a detailed calculation of centrifugal force generated when a vehicle travels on a curved road. There are two types of curves: horizontal curves and vertical curves. In both types of curves, although the centrifugal force is the same when the vehicle moves, the direction of the force relative to the horizontal plane differs.
Horizontal Curve
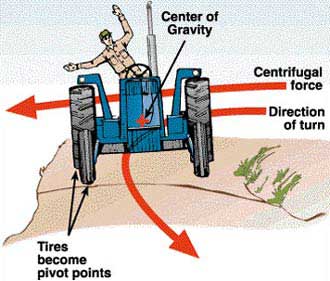
When a vehicle travels on a curved road, a centrifugal force appears originating from the vehicle’s center of gravity, acting horizontally, directed from the center of the curve outward. The magnitude of the centrifugal force equals the vehicle’s mass multiplied by the square of the velocity divided by the radius of the curve.
 |
|
Diagram illustrating centrifugal force when entering a curved road. (Muextension) |
For example, for a vehicle weighing 5,000 kg traveling on a curve with a radius of 50 m at a speed of 50 km/h, which is equivalent to 13.89 m/s, the square of the speed equals 192.9 (m/s)². The centrifugal force will therefore be 19,290 N, acting on the vehicle’s center of gravity horizontally, directed outward from the center of the curve. In addition to the centrifugal force, the vehicle also experiences gravitational force. The gravitational force equals the vehicle’s mass multiplied by the acceleration due to gravity (g=10 m/s²). The centrifugal force and gravitational force combine to form a resultant force.
This resultant force also originates from the vehicle’s center of gravity, pulling it downwards at an angle. The contact point with the road will have a distance from the center of the vehicle’s base equal to the height of the vehicle’s center of gravity above the road multiplied by the ratio of the centrifugal force to the vehicle’s gravitational force. In the example above, the ratio of centrifugal force to gravitational force is 0.39. If the vehicle’s center of gravity is 1.5 m above the road, then the distance from the contact point of the resultant force to the center of the vehicle’s base is 0.585 m. In this case, if the vehicle’s base width is less than twice this distance (i.e., less than 1.17 m), the vehicle will tip over towards the side opposite the center of the curve. The base width of the vehicle is the distance between the outer edges of the wheels.
In the same scenario, if the vehicle travels at 80 km/h (22.22 m/s), the centrifugal force will nearly double to 49,372 N. The contact point of the resultant force will be 1.5 m from the center of the base. If the vehicle’s width is less than 3 m, it will tip over.
Thus, four factors can be identified that influence the tipping phenomenon. First, the higher the speed, the more dangerous it becomes. As seen in the example, a 60% increase in speed results in a 160% increase in centrifugal force. Second, the smaller the curve radius, the more adverse the effects. Third, the heavier and taller the vehicle, the more dangerous it is, as its center of gravity is higher relative to the road. Finally, the narrower the base, the easier it is for the vehicle to tip over.
This explains the accident involving the E1 train, as although the curve radius of the railway is typically no less than 100 m, the distance between the two rails (the width of the base) is often no more than 1.2 m, making it easier for the resultant force of gravitational and centrifugal forces to pull outside the base, leading to the train tipping over. Therefore, on railway sections with a curve radius of 100 m, speed must typically be limited to below 60 km/h. If the speed exceeds 60 km/h, accidents become unavoidable.
Vertical Curve:
This refers to a road with a straight section on the horizontal plane but is either bulging upward or dipping downward. In this case, the centrifugal force is still calculated as above and originates from the vehicle’s center of gravity, but it has a vertical direction, acting from the bottom to the top if the curve bulges upward, or from the top to the bottom if the curve dips downward.
For example, for a vehicle weighing 5,000 kg traveling at a speed of 60 km/h on a vertical curve that bulges upward, with a curve radius of 50 m, the centrifugal force equals 27,750 N, acting vertically from the bottom to the top. The gravitational force of the vehicle remains as above at 50,000 N. Since the centrifugal force and gravitational force act in opposite directions, the effective gravitational force on the vehicle is reduced to 22,250 N, meaning the vehicle feels much lighter, akin to driving on a slippery road, with the friction coefficient reduced by more than half, making it prone to sliding sideways due to the sudden lightness of the steering. In this same case, if the vehicle travels at 80 km/h, the centrifugal force will be 49,327 N, which is nearly equal to the gravitational force. At this point, the vehicle will hardly stick to the road, feeling as though it is being lifted, resulting in the steering becoming ineffective and the vehicle becoming completely unstable, rolling sideways due to inertia.
Associate Professor Dr. Nguyen Duy Hanh