Throughout human history, there has been a rather mysterious number that has fascinated many people. Over generations, from ancient times to modernity, numerous extraordinary minds have sought to calculate this number, only to find that they can only approximate it.
Exploring the History of the Transcendental Number
This number cannot be expressed as a finite integer, a fraction, or an irrational number. To date, it is accepted as a transcendental number.
1. Definition
p = 3.141592653589793238462643383279….
Pi is the name of the 16th letter of the Greek alphabet. It is defined as a constant, the ratio of the circumference of a circle to its diameter.
The name pi comes from the word peripheria, which means the circumference of a circle.
However, it does not have a precise name; it is often referred to as p, c, or just p.
The letter p was used around the mid-18th century, after Euler published his analytical treatise in 1748. The intention of using the symbol p was to honor the Greek mathematicians who first found an approximate value for pi.
By the end of the 20th century, pi had been calculated with accuracy up to the 200 billionth digit (200,000,000,000).
On September 11, 2000, the one trillionth (1,000,000,000,000) decimal of pi was revealed to be 0.
The simplest definition given for this famous number is: it is the ratio of the area of a circle to the square of its radius. For example, the area of the circle shown here is p times the area of the square.
The same number is also found in the calculation of the circumference of a circle, which is equal to 2p times its radius. As Archimedes observed, this number is used in both calculations. It is also not surprising to encounter this number here and there.
* The area of the annulus formed between two circles with approximately equal radii can be calculated in two ways:
- The area of the larger circle minus the area of the smaller circle.
- Since the radii of the two circles are nearly equal, the area of the annulus can also be calculated as the product of the circumference of one of the circles and the thickness of the annulus.
2. Methods of Calculating Pi
Approximation Calculations.
The oldest method.
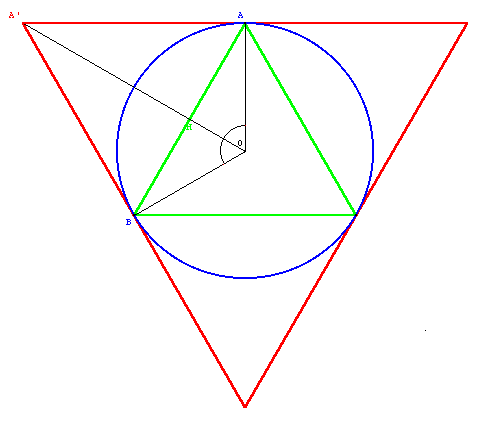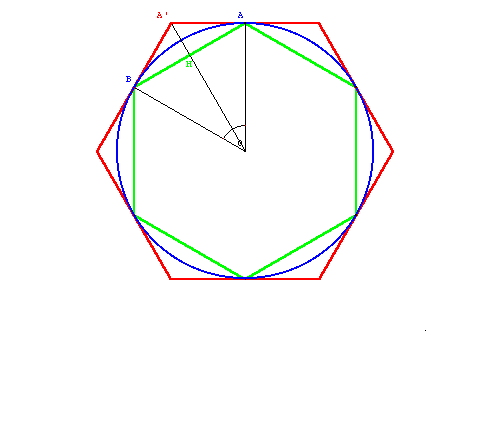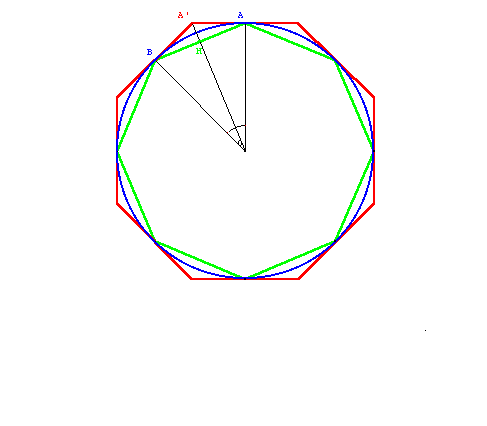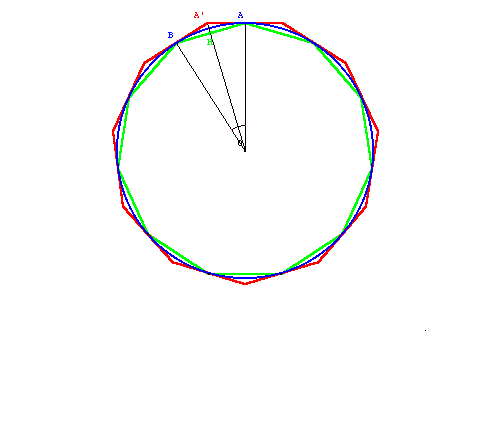
Draw a circle with a radius of 1 unit and inscribe and circumscribe regular polygons around the circle.
If the polygon is a square, then the circumference of the circle will be between the circumferences of the inscribed and circumscribed squares, meaning the value of Pi will be:
2
2.828
Increasing the number of sides to 6 yields a better result: 3 (since the side of the hexagon equals the radius of the circle) and 2 = 3.461…:
3
3
When calculating the circumference of polygons with thousands of sides and dividing the result by the diameter of the circle, the most accurate approximation of 
is found to be 355/113.
A memorable number: the first odd numbers, two 3s, two 5s, two 1s, and the total of the two numbers in the numerator and denominator crossing each other equals 6.
The Babylonians calculated the value of pi by comparing the circumference of a circle to an inscribed polygon, approximating it to 3 times the diameter of the circle. They estimated: p = 3 + 1/8 (which is 3.125).
Archimedes used a polygon with 96 sides to find a lower estimate of 3 + (10/71) = 3.1408… and an upper estimate of 3 + (1/7) = 3.1429…
This means: 3.1408…
To determine the value of Pi, one could attempt to draw a circle and a square with equal areas using a ruler and compass. Using the same tools, one could also draw a line segment with a length of Pi and deduce the exact value of this number.
However, this method of drawing is unattainable: In 1837, Pierre Wantzel proved that it is only possible to construct line segments with a ruler and compass when the length is an algebraic number, meaning a solution to an algebraic equation with integer coefficients. In 1882, Ferdinand von Lindemann proved that Pi is not an algebraic number.
Pi Appears in Many Areas of Mathematics
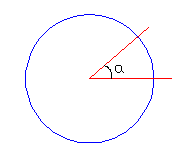* For example, when measuring angles, one must choose a unit by defining a complete circle as 360 degrees, then with the unit “degree,” the measure is 1/360 of a circle. If one uses the value of a full circle as 2p, the unit of measurement will be called a radian and have a value of 1/(2p). Measuring angles in radians has many advantages: for example, the length of a segment of the circle bounded by angle a will equal the radius when measured in radians, but if measured in degrees, it will equal (2pra)/360.
* Similarly, the ratio (sin x)/x approaches 1 as x approaches 0 when angles are measured in radians, but approaches 180/p when angles are measured in degrees.
* The use of radians for measuring angles leads to many properties of Pi; for instance, according to Euler’s theorem, the exponential of the complex number 2ip is equal to 1. From the results of using radians to calculate angles, Pi is found in unexpected places: for example, the infinite series (Leibniz series)
1 – (1/3) + (1/5) – (1/7) – … equals p/4.
* Integrals:
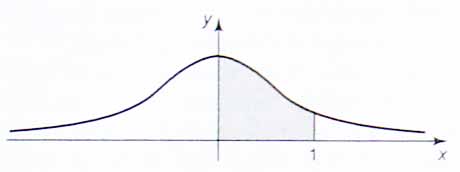
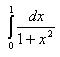the area under the curve of the equation f(x) = 1/(1+ x^2) between 0 and 1 also equals p/4. Both results are easily explained since the tangent of the angle p/4 equals 1.
Pi also appears in the value of the infinite sum.
1 + (1/22) + (1/32) + (1/42) + … equals p/6.
The Odd Numbers of Pi
The number Pi summarizes a history of mathematics spanning over 4000 years, encompassing Analytical Geometry and Algebra. Mathematicians have admired it since the time of Ancient Civilizations, particularly the Greeks in their geometric concerns. The oldest known value of Pi used by humanity has been certified from a tablet.
Later, continuous research efforts:
* Archimedes calculated Pi = 3.142 with an accuracy of 1/1000. The formula was: 3 + 10/71.
The Archimedes method was used for 2000 years.
* In the Bible, around 550 BC, this number was hidden in a verse on a tablet from ancient Babylonia (located in Iraq) written in cuneiform script, discovered in 1936, and the tablet dates back 2000 years before Christ. After much curiosity and research, the value Pi was found to be 3.141509.
* Around 1450, Al-Kashi calculated Pi with 14 decimal places using the polygon method of Archimedes.
This was the first time in human history that Pi was calculated with over 10 decimal places.
* In 1609, Ludolph von Ceulen, using Archimedes’ method, calculated Pi with 34 decimal places, which were then engraved on his tombstone.
It is impossible to calculate the exact value of Pi.
By the late 18th century, Johann Heinrich Lambert (1728-1777) and Adrien-Marie Legendre (1752-1833) proved that there is no fraction that can represent Pi.
In the 19th century, Lindemann proved that Pi cannot be a solution to any algebraic equation with integer coefficients (for example, y = ax2 + bx + c where a, b, c are integers).
* Following Ludolph von Ceulen, through the diligent research of mathematicians:
Newton (1643-1727)
Leibniz (1646-1716)
Gregory (1638-1675)
Scientists such as Euler (1707-1783), Gauss, Leibniz, Machin, Newton, and Viète sought formulas to accurately calculate the approximate value of π (Pi). The simplest formula discovered by Leibniz in 1674 is: π/4 = 1 – 1/3 + 1/5 – 1/7 + …
Carl Louis Ferdinand von Lindemann (1852-1939)
Srinivasa Aiyangar Ramanujan (1887-1920)
William Shanks (1812-1882) calculated π with 707 decimal places in 1874.
It wasn’t until the 18th century and early 20th century that Pi was calculated to an accuracy of 1,000 decimal places. In 1995, Hiroyuki Gotu set a world record by discovering 42,195 decimal places.
Where Did the Symbol π (Pi) Come From?
According to the mathematician and historian Florian Cafori (1859-1930), the first person to use the Greek letter in geometry was William Oughtred (1575-1660). To denote circumference, which in English is “periphery,” he used the Greek letter Pi (π). To indicate diameter, which in English is “diameter,” he used the Greek letter Delta.
In 1760, William Jones (1675-1749) used the letter Pi (π) in his book Synopsis Palmariorum Matheseos to refer to the ratio of circumference to diameter of a circle.
It was not until the renowned Swiss mathematician Leonhard Euler began using the symbol Pi (π) widely in 1748 that it was accepted by everyone as the ratio of circumference to diameter of a circle, as noted in his book Introductio in analysin infinitorum.
The Fascination with the Mysterious Number
The first one hundred decimal places of Pi:
3.141 592 653 589 793 238 462 643 383 279 502 884 197 169 399 375 105 820 974 944 592 307 816 406 286 208 998 628 034 825 342 117 0679 …
Daniel Morin recorded 2,000 decimal places of Pi at http://platon.lacitec.on.ca/~dmorin/divers/pi.html
100,000 decimal places can be found on Yves Martin’s page: http://www.nombrepi.com/pi100000.html
In 1995, Yves Martin used an EPSON laptop running at 10 MHz to execute the PIF.EXE program written in Pascal, which ran for 1 hour, 28 minutes, and 33 seconds to produce 130,000 decimal places of Pi.
On September 19, 1995, at 12:29 AM local time GMT-04, Canadian mathematician Simon Plouffe, in collaboration with Peter Borwein and David Bailey, discovered a formula for calculating Pi that challenged previously held beliefs about its calculation.
This formula, known as the BBP formula, allows for the calculation of the decimal places of Pi independently, which was previously thought to be impossible.
On Monday, September 22, 1997, Fabrice Bellard set a record by calculating the trillionth decimal place of Pi using Plouffe’s BBP formula and his own accelerated computation methods.
On February 3, 1999, Colin Percival reached the 40 trillionth decimal place using Bellard’s formula.
On September 11, 2000, the million-trillionth decimal place was revealed to be zero: (one million trillion = 1,000,000,000,000,000).
Now, with computers running thousands of times faster, Pi can only be approximated, as the sequence of decimal places continues indefinitely.
