We are taught that the Earth’s orbit is elliptical, so when the Earth is farther from the Sun, it experiences winter, and when it is closer, it experiences summer. In reality, this is not entirely accurate.
Most people still believe that in summer, the Earth is closer to the Sun than in winter. This is true for summer in the Southern Hemisphere but not for summer in the Northern Hemisphere.
In the Southern Hemisphere, summer brings the Earth about 5 million kilometers closer to the Sun than in winter, but this is the opposite in the Northern Hemisphere. The average distance between the Earth and the Sun is 150 million kilometers, and the main reason the Earth experiences seasons is due to its axial tilt relative to its orbital plane, causing each pole to occasionally tilt closer to the Sun and at other times, farther away from it.
Furthermore, the Earth’s orbit is referred to as elliptical but is actually only slightly flattened compared to a perfect circle. Despite this, it is often illustrated as the shape of an egg. So how can we accurately visualize the shape of the Earth’s orbit?
Senior lecturer Stephen Hughes at the School of Mathematics and Physics, University of Queensland, Australia, scaled down the ratio to compare the shape of the Earth’s orbit to a bicycle wheel with a diameter of 66 cm and consulted a technician at a bicycle shop about the actual deformation of a bicycle rim. The results were quite surprising.
The Earth’s orbit is very close to a perfect circle. If this orbit were represented as a bicycle wheel with a diameter of 66 cm, it would only be flattened by 0.1 mm compared to a perfect circle. This thickness of 0.1 mm is equivalent to a thin layer of paint, making it virtually indistinguishable from a perfect circle with the naked eye.

If the Earth’s orbit were a bicycle rim with a diameter of 66 cm, its deformation compared to a perfect circle would be merely a thin layer of paint. (Photo: Stephen Hughes).
Mr. Hughes also examined the orbits of other planets for a broader perspective. The orbits of Venus and Neptune are also nearly perfect circles. The deformation of Venus’s orbit is only 14 μm, and Neptune’s is just 31 μm (1 μm or 1 micrometer is one-millionth of a meter).
The two planets with the least circular orbits are Mars and Mercury. If Mars’s orbit were reduced to the size of a 66 cm bicycle rim, the deformation would be less than 3 mm, a flattening that would be hardly noticeable while riding this bike. Mercury has the flattest orbit, with a deformation of 14 mm, which is only 2%.
Minimal Deformation
Thinking mathematically, after reading the above, you might have a question: If the average distance between the Earth and the Sun is 150 million km and this distance varies by 5 million km depending on the time of year, doesn’t that mean the deformation of the orbit compared to a perfect circle is only a little over 3%?

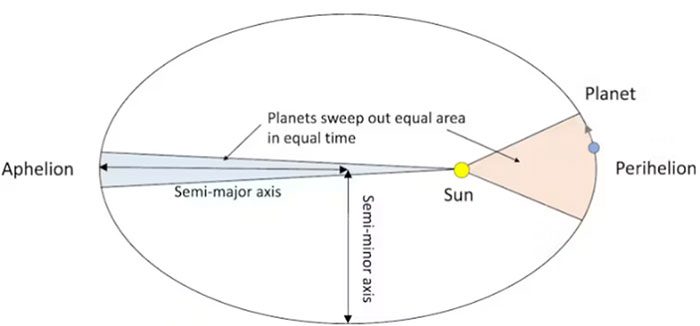
The actual shape of the Earth’s orbit: almost a perfect circle. The length a is the semi-major axis, and the length b is the semi-minor axis of the ellipse. Aphelion (the farthest point) is the maximum distance, and perihelion (the nearest point) is the minimum distance from the Earth to the Sun (Photo: Stephen Hughes).
The answer is that the Sun is not located at the center of the ellipse but is offset to one side at a focal point. If during the formation process, a planet moves at precisely the right speed to counteract gravitational forces, it will move in a circle.
However, in reality, planets rarely move at a steady speed that would allow them to trace a circular orbit. Sometimes they move faster, and sometimes slower, which results in an elliptical shape.
Close to a Perfect Circle
Thousands of years ago, ancient Greeks believed that all celestial objects revolved around the Earth in perfect circles. This belief persisted until the Polish astronomer Nicolaus Copernicus (1473-1543) discovered that the planets, including Earth, actually revolve around the Sun.
Astronomer Copernicus believed that the orbits of planets were circular. Later, the German astronomer and mathematician Johannes Kepler (1571-1630) found that Copernicus was wrong and proposed three laws of planetary motion.
The first law states that the orbits of planets are elliptical rather than circular. The third law relates the size of a planet’s orbit to the time it takes for that planet to complete its orbit in a very complex way that is unnecessary to discuss here.
The second law describes the speed at which each planet moves along its orbit. If you draw a straight line from the Sun to any planet, as that planet moves, this line will sweep out an area that takes the same time for one planet to traverse as another planet passing through the swept area. This is because planets move faster when they are closer to the Sun.
The main reason books illustrate orbits as distinctly elliptical is to demonstrate Kepler’s second law. If the Earth’s orbit were drawn to scale, the naked eye would not be able to discern any differences between the swept areas.
Illustrations in books often lead to the misconception that Earth’s orbit around the Sun looks like this. (Photo: Stephen Hughes).
However, depicting the orbit so exaggeratedly can mislead viewers into thinking that the Earth’s orbit is very flat.
While the ancient Greeks were mistaken in believing that the Earth is the center of the Solar System, they were not far off regarding the shape of the planets’ orbits. Thus, if we disregard the exaggerated illustrations meant to simplify Kepler’s second law, we can say that the Earth’s orbit is circular.