Conservation laws are extremely useful in physics. Essentially, when a specific measurable property of an isolated physical system does not change over time (and is conserved), it is described by a conservation law.
Conservation laws are useful in various fields of physics, but sometimes they can become quite complex. This is where a theorem developed by a German female mathematician in the 1910s becomes helpful. Noether’s Theorem connects symmetry laws and conservation laws, and it can be described as one of the most beautiful theorems in physics.

Portrait of Emmy Noether around 1900.
Amalie Emmy Noether was a German mathematician whose work focused particularly on algebra. Her contributions also had a significant impact on a branch known as mathematical physics – a field related to the development of mathematical methods in physics.
The development of many physical laws is based on something very abstract, the concept of symmetry. Symmetry can mean different things in different fields; in geometry, geometric shapes can be symmetrical, in chemistry, molecules can be symmetrical, but symmetry also means something different in physics.
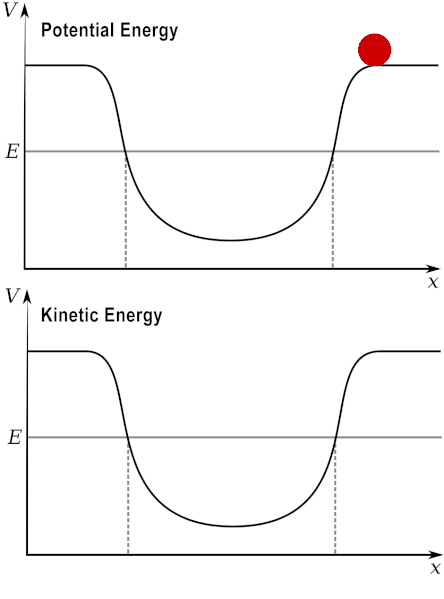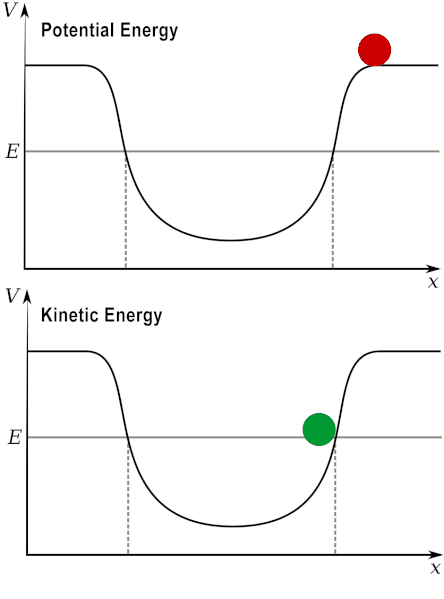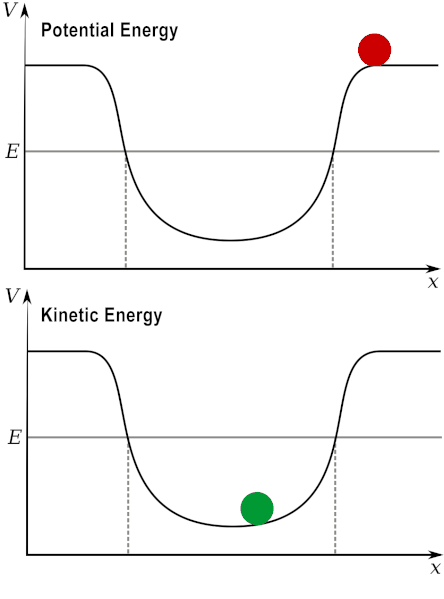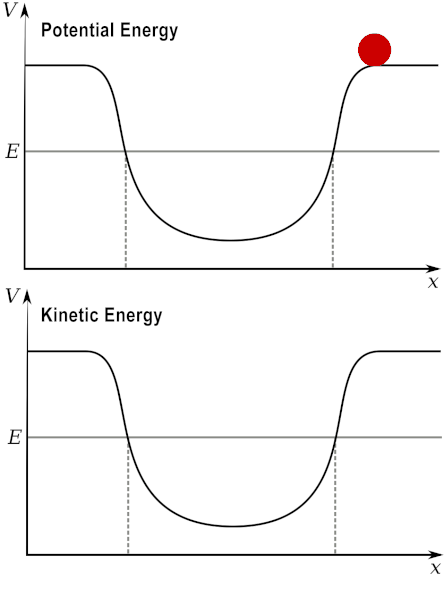
When you throw a ball upwards with an initial velocity, its kinetic energy will then convert into potential energy. Think of it this way: kinetic energy depends on motion, while potential energy depends on position; when you throw the ball up, it starts with a lot of energy in motion – it will rise. Then, when it reaches its maximum height, it has no kinetic energy, as it has stopped (and then falls down) – at that moment, it only has potential energy.
In other words, potential energy transforms into kinetic energy, and kinetic energy transforms back into potential energy.
If you set up a kinetic-potential energy experiment, the experiment will work the same way if you repeat it under the same conditions. And in subsequent trials at later times, you will still get the same result – this means that the energy conservation level remains the same regardless of time. In other words, the time transformation does not change the system at all. The case where nothing changes in the physical laws/features of a system even with the action of a transformation is called symmetry.
In 1918, Emmy Noether published a paper connecting symmetries and conservation laws. After that, the career of this German mathematician showed signs of brilliant development. Her interest in mathematics came from her father, a mathematics professor at the University of Erlangen. Noether then went on to become both a student and a professor – but worked without pay. Emmy Noether was relatively unknown despite her significant contributions to science at the time; Noether’s Theorem unified ideas that had been slowly developed over centuries by René Descartes, Gottfried Leibniz, Isaac Newton, and Joseph-Louis Lagrange.
Not stopping there, Noether published an important mathematical paper discussing transformation groups but did not directly discuss their relationship with physics. Her work was divided into two theorems, the first theorem providing a global relationship between continuous symmetries and conservation laws, while the second theorem applies to systems with local symmetries.
The ball experiment related to conservation laws is the simplest example. Energy is conserved due to symmetry in the translation over time. Now consider a more complex idea of the conservation of angular momentum (the momentum of a rotating object). Ice skaters are masters of this conservation: they know that if they spin with their arms tucked in, it makes them spin faster – and if they extend their arms, their spinning speed will decrease.
Think of it this way: angular momentum is mass times velocity times radius (L = m * v * r). The mass of an ice skater remains constant, so if the radius increases, the speed must decrease to compensate for that, and vice versa.

Ice skater.
So what is symmetry in this case? If momentum is conserved, then space must be isotropic. This means that if there are no external torques (angular forces), angular momentum does not change. Simply put, isotropy means that everything looks the same even when you rotate it. For example, a perfect sphere, without any blemishes, is invariant when rotated; no matter how you spin it, it still looks the same.
Believe it or not, this relates to one of the most important theories in physics: general relativity.
Mass Curves Spacetime
General Relativity (GR) is the theory that describes gravity with high precision. During its development, Emmy Noether contributed to the interpretation of the theory.
From 1915 to 1918, she engaged in debates with David Hilbert, Felix Klein, and Einstein himself about conservation equations in GR. Einstein proposed an expression quite similar to the energy conservation expression we are more familiar with. However, one component of the equation is invariant under a specific transformation known as an affine transformation. Affine transformations preserve parallel structure like a symmetry leaf. This was not expected from a general equation that was supposed to encompass the big picture of energy conservation.

In 1918, Klein pointed out the difference between Einstein’s field equations and ordinary energy conservation. Einstein disagreed, believing that conservation similar to classical mechanics was at least partly contained in his equations.
For Hilbert, a leading mathematician of his time, the fact that GR did not show a simple kind of energy conservation was simply because… it was so. Noether, and later Klein, agreed that there were no conservation laws in General Relativity, and that conclusion stemmed from her famous theorem.
From Noether’s second theorem, matter in GR shows a conservation similar to energy and momentum conservation, but without a motion equation. In fact, any theory that is similar for any coordinate system shows a strange conservation law, a law that does not provide solutions through direct physical interpretations.
Supersymmetry
Noether’s symmetry theorem has also been applied in several other areas of physics.
The Standard Model of particle physics divides particles into two types: fermions and bosons. All known fermions (the particles that make up ordinary matter) have half-integer spin. The spin number describes how many symmetrical faces a particle has in a complete rotation; a spin of 1/2 means the particle must be spun twice (through 720°) before it has the same configuration as when it started.
Meanwhile, bosons, which are not matter particles, have integer spins (0, 1, 2, etc.). Spin is a property of particles that indicates where they will be if immersed in a magnetic field. A proposed theory called Supersymmetry (SUSY) suggests that for every discovered fermion, there will be a supersymmetric boson with similar properties.
This makes things more certain, but it also simplifies everything significantly. The lightest particle of SUSY would make up a wonderful dark matter particle. Furthermore, other particles can be predicted from SUSY, although none of them have been observed experimentally.
According to Noether’s theorem, conservation can be found if it is connected to symmetry. The conservation quantities of SUSY are charges, a kind of general idea about charges as we understand them.
Recognition
Her contributions to mathematics are immense, especially concerning her short life.
Noether had to struggle in a male-dominated society like most female scientists of her time. As one of the most distinguished scientists, her talent was the most fundamental thing that earned her colleagues’ respect. But that was still not enough.
Unfortunately, Noether still needed the support – or perhaps we should call it the endorsement – of prominent mathematicians valued by universities. Hilbert was involved in this; he persuaded others to accept her at Göttingen, stating, “I do not see that gender is a barrier to recognizing her talent.”
Noether’s theorem is referred to as “one of the most important mathematical theorems ever proven in guiding the development of modern physics.” Her contributions to mathematics are immense, particularly considering her short life. She discovered one of the most elegant, and arguably profound ideas in modern physics, often facing significant adversity from male-dominated fields. This is certainly something worth knowing if you are interested in science.